KS4 Curriculum
- KS4 Acting
- KS4 Art and Design: Art, Craft and Design
- KS4 Art and Design: Photography
- KS4 Art and Design: Textiles
- KS4 Child Development
- KS4 Computer Science
- KS4 Dance
- KS4 Engineering
- KS4 English
- KS4 Enterprise and Marketing
- KS4 Food Preparation and Nutrition
- KS4 Geography
- KS4 Graphics
- KS4 History
- KS4 Maths – Foundation
- KS4 Maths – Higher
- KS4 Modern Foreign Languages
- KS4 Music
- KS4 Music – Rock School Limited
- KS4 Science
- KS4 Sociology
- KS4 Core PE
- GCSE PE / CNAT PE
- KS4 Religious Studies
- KS4 Product Design
Home > Curriculum > [wpseo_breadcrumb]
KS4 Maths – Higher
Please click on the links below to find out more about each unit.
| Year Long Term Objective: To Build upon the foundation laid in KS3 to prepare students for the rigours of the GCSE. Students should be stretched with challenging GCSE style questions routinely. | ||||||
| Year | Autumn 1 | Autumn 2 | Spring 1 | Spring 2 | Summer 1 | Summer 2 |
| 10 |
Number | Fractions, Ratio and Percentages | Graphs | Transformations and Constructions | Probability | Similarity and Congruence |
| 11 |
Algebra | Angles and Trigonometry | Area and Volume | Equations and Inequalities | Multiplicative reasoning | More Trigonometry |
Number
Overview
– Place value and estimating
– HCF and LCM
– Calculating with powers (indices)
– Zero, negative and fractional indices
– Powers of 10 and standard form
– Surds
Example Key Words
Significant figure
The first non zero digits of a number
Factors
A number that divides exactly into another number
Multiple
A value in the number’s time table
Indices
Indices show how many times a number or letter has been multiplied by itself.
Standard Form
A way of writing very large and very small numbers using a power of 10
Surd
A surd is an expression that includes a square root and the value is an irrational number
Fractions, Ratio and Percentages
Overview
– Fractions
– Ratios
– Ratio and proportion
– Percentages
– Fractions, decimals and percentages
Example Key Words
Numerator
The top number of a fraction
Denominator
The bottom number of a fraction
Equivalent fraction
Fractions that are equal in size but are written differently
Simplest terms
A fraction in its simplest terms cannot be cancelled down
Percent
Out of one hundred
Percentages and fractions
Percentages are fractions with a denominator of 100
Graphs
Overview
– Linear graphs
– Graphing rates of change
– Real-life graphs (To include phone bills and taxi charges)
– Line segments
– Quadratic graphs
– Cubic and reciprocal graphs
Example Key Words
Linear graph
A straight line graph
Gradient
The measure of the steepness of a curve.
Y intercept
The point where the line crosses the y axis
Distance- time graph
A graph that plots the distance traveled by an object on a vertical axis against the time taken
Quadratic graph
Involves an x2 and will be the shape of a parabola
Cubic and reciprocal
Involves an x3 (cubic) and 1/x (reciprocal)
Transformations and Constructions
Overview
– 3D solids
– Reflection and rotation
– Translation and enlargement (To include computer generated imagery and vectors)
– Combinations of transformations
– Bearings and scale drawings
– Constructions
– Loci
Example Key Words
Transformation
A change in the position, size or shape of a figure
Bearing
Measuring the angle from one postion to another. Written as a 3 digit number, measured from the north line, in a clockwise direction.
Scale Drawing
A drawing that shows a real object with accurate sizes in proportion to the reduced or enlarged by a certain amount (called the scale)
Construction
Turning a shape around a fixed point.
Loci
This changes the size of the shape – it can make it smaller.
Scale factor
A drawing which has been reduced or enlarged from its original size, to a specified scale
Probability
Overview
– Combined events
– Mutually exclusive events
– Experimental probability
– Independent events and tree diagrams
– Conditional probability
– Venn diagrams and set notation
Example Key Words
Probability
The likelihood or chance of a given event happening. Often expressed as a fraction, decimal or percentage.
Experimental probability
A calculation obtained from an experiment.
Venn diagram
A diagram that represents sets and shows where those sets intersect.
Probability tree diagram
A tree diagram is used to determine and visualise all the outcomes and probabilities of 2 or more events
Mutually exclusive
A and B are mutually exclusive events if they cannot occur at the same time. This means that A and B do not share any outcomes
Independent events
Two events are independent if the occurrence of one event does not affect the chances of the occurrence of the other event.
Similarity and Congruence
Overview
– Congruence
– Geometric proof and congruence
– Similarity
– Similarity in 3D solids
Example Key Words
Congruent
Congruent shapes are shapes that are exactly the same. The corresponding sides are the same and the corresponding angles are the same.
Similar
Two shapes are said to be similar if they are exactly the same shape, but are different in size. All sides are in the same proportion defined by the scale factor.
Similarity in area and volume
If 2 shapes are similar and the scale factor of the lengths is x, then the scale factor of the area is x2 and the scale factor iof the volume is x3
Algebra
Overview
– Algebraic indices
– Expanding and factorising
– Equations
– Formulae
– Linear sequences
– Non-linear sequences
Example Key Words
Expanding brackets or multiplying out brackets
This involves mulitplying each term inside the bracket by the number/letter outside the bracket or inside a second bracket
Factorising
The opposite of multiplying out brackets, involves putting the expression into bracket(s)
Formula
An equation that expresses a mathematical relationship between two or more variables
Term of a sequence
A number in a sequence
Linear sequences
The term to term rule is a constant number and the nth term rule just involves “n”
Non- linear sequence
Generally a quadratic sequence where you need to find the 2nd difference and the nth term rule will involve “n2”
Angles and Trigonometry
Overview
– Angle properties of triangles, quadrilaterals and parallel lines
– Interior angles of a polygon
– Exterior angles of a polygon
– Pythagoras’ theorem
– Trigonometry
Example Key Words
Hypotenuse
The longest side of a triangle. It is also the side opposite the right angle.
Pythagoras' Theorem
A theorem stating that in a right triangle the area of the square on the hypotenuse is equal to the sum of the areas of the squares drawn on the other two sides.
Opposite and adjacent side Side
The side opposite (opposite) and next to (adjacent) the angle you are dealing with in a triangle (not the right angle)
The Sine ratio
The sine of an angle in a right triangle is defined as the ratio of the length of the side opposite the angle to that of the hypotenuse.
The Cosine ratio
The cosine of an angle in a right triangle is defined as the ratio of the length of the side adjacent to the angle to that of the hypotenuse.
The Tangent ratio
The tangent of an angle in a right triangle is defined as the ratio of the length of the side opposite the angle to that of the adjacent side.
Area and Volume
Overview
– Perimeter and area
– Units and accuracy
– Prisms
– Circles
– Sectors of circles
– Cylinders and spheres
– Pyramids, cones and spheres
Example Key Words
Surface area
The sum of the areas of all faces of a solid figure
Prism
A 3D shape that has the same cross sectional throughout the length of the shape.
Circumference of a circle
The perimeter of a circle.
Radius and Diameter of a circle
The radius is a straight line from the centre to the circumference. The diameter goes from one side of the circle to the other passing through the centre.
Sector of a circle
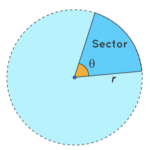
Segment of a circle
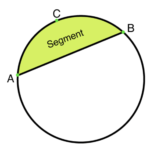
Equations and Inequalities
Overview
– Solving quadratic equations
– Completing the square
– Solving simultaneous equations
– Solving quadratic simultaneous equations
– Solving linear and quadratic inequalities
Example Key Words
Variable
A symbol that stands for an unknown quantity
Equation
A mathematics statement that uses an equals sign to show that two expressions are equal.
Inequality
A relationship between two expressions that are not equal, often written with the symbols >, >, <, and <
Quadratic
An expression or equation that includes an x²
Simultaneous equations
A set of two or more equations that contain two or more unknown quantities
Completing the square
A way of simplifying or solving a quadratic equation by adding an expression to both sides to make one part of the equation a perfect square.
Multiplicative reasoning
Overview
– Growth and decay (To include loan sharks and exponential growth in diseases)
– Compound measures
– Ratio and proportion
Example Key Words
Compound Interest
The amount of interest earned each year is added onto the original capital and included in the following year’s calculation
Simple interest
The total amount of interest is added on at the end the term
Depreciation
The reduction in value of an asset over time.
Growth and decay
Using a compound interest type formula to calculate the growth of a population or depeciation of an asset
Direct Proportion
A direct relationship between the increase or decrease of two variables.
Inverse proportion
The relationship between one variable is directly proportional to the reciprocal of another.
More Trigonometry
Overview
– Accuracy
– Graph of the sine and Cosine functions
– The tangent function
– Calculating areas of non right angled triangles
– Using the Sine and Cosine rules
– Solving problems in 3D
– Transforming trigonometric graphs
Example Key Words
Area of a non right-angled triangle
Area = 1/2abSinC
